Ряди Лорана ізольовані особливі точки і їх класифікація. Ізольовані особливі точки, їх класифікація Знаходження особливих точок

особлива точка

в математиці.

1) Особлива точка кривої, заданої рівнянням F ( x, у) = 0, - точка М 0 ( х 0, y 0), В якій обидві приватні похідні функції F ( x, у) Звертаються в нуль:

Якщо при цьому не всі другі приватні похідні функції F ( x, у) В точці М 0 дорівнюють нулю, то О. т. Називають подвійний. Якщо поряд зі зверненням в нуль перших похідних в точці М 0 звертаються в нуль і всі другі похідні, але не всі треті похідні дорівнюють нулю, то О. т. Називається потрійною, і т.д. При дослідженні будови кривої поблизу подвійний О. т. Важливу роль грає знак вираження

Якщо Δ> 0, то О. т. Називається ізольованою; наприклад, у кривій у 2 - х 4 + 4x 2= 0 початок координат є ізольована О. т. (Див. Мал. 1 ). Якщо Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4= 0 початок координат є вузлова О. т. (Див. Мал. 2 ). Якщо Δ = 0, то О. т. Кривої є або ізольованою, або характеризується тим, що різні гілки кривої мають в цій точці загальну дотичну, наприклад: а) точка повернення 1-го роду - різні гілки кривої розташовані по різні боки від загальної дотичній і утворюють вістря, як у кривої у 2 - х 3= 0 (див. Мал. 3 , a); б) точка повернення 2-го роду - різні гілки кривої розташовані по одну сторону від загальної дотичній, як у кривої (у - x 2)2 - х 5= 0 (див. Мал. 3 , Б); в) точка самопрікосновенія (для кривої у 2 - х 4= 0 початок координат є точкою самопрікосновенія; (Див. Мал. 3 , В). Поряд із зазначеними О. т. Є багато інших О. т. Із спеціальними назвами; наприклад, асимптотична точка - вершина спіралі з нескінченним числом витків (див. Мал. 4 ), Точка припинення, кутова точка і т.д.

2) Особлива точка диференціального рівняння - точка, в якій одночасно звертаються в нуль і чисельник і знаменник правої частини диференціального рівняння (Див. Диференціальні рівняння)

де Р і Q - безперервно диференціюються функції. Припускаючи О. т. Розташованою на початку координат і використовуючи Тейлора формулу (Див. Тейлора формула), можна уявити рівняння (1) у вигляді

де P 1 ( x, у) І Q 1 ( x, у) - нескінченно малі по відношенню до

Саме, якщо λ 1 ≠ λ 2 і λ 1 λ 2> 0 або λ 1 = λ 2, то О. т. Є вузол; всі інтегральні криві, що проходять через точки досить малій околиці вузла, входять в нього. Якщо λ 1 ≠ λ 2 і λ 1 λ 2 i β, α ≠ 0 і β ≠ 0, то О. т. Є фокус; всі інтегральні криві, що проходять через точки досить малій околиці фокусу, являють собою спіралі з нескінченним числом витків в будь-який як завгодно малій околиці фокусу. Якщо, нарешті, λ 1,2 = ± iβ, β ≠ 0, то характер О. т. не визначається одними лінійними членами в розкладах Р ( х, у) І Q ( x, у), Як це мало місце у всіх перерахованих випадках; тут О. т. може бути фокусом або центром, а може мати і більш складний характер. В околиці центру все інтегральні криві є замкнутими і містять центр всередині себе. Так, наприклад, точка (0, 0) є вузлом для рівнянь у" = 2у / х(Λ 1 = 1, λ 2 = 2; див. Мал. 5 , А) і y" = у / х(Λ 1 = λ 2 = 1; див. Мал. 5 , Б), сідлом для рівняння у "= -у / г(Λ 1 = -1, λ 2 = 1 ; см. Мал. 6 ), Фокусом для рівняння у "=(х + у) / (х - у) (Λ 1 = 1 - i, Λ 2 = 1 + i; см. Мал. 7 ) І центром для рівняння у "= -x / y(Λ 1 = -i, Λ 2 = i; см. Мал. 8 ).

Якщо х, у) і Q ( х, у) Аналітичні, околиця О. т. Вищого порядку може розпадатися на області: D 1 - заповнені інтегральними кривими, обома кінцями входять в О. т. (Еліптичні області), D 2 - заповнені інтегральними кривими, одним кінцем входять в О. т. (параболічні області), і D 3 - області, обмежені двома інтегральними кривими, що входять в О. т., між якими розташовані інтегральні криві типу гіпербол (гіперболічні області) (див. Мал. 9 ). Якщо немає інтегральних кривих, що входять в О. т., То О. т. Називається точкою стійкого типу. Околиця стійкою О. т. Складається з замкнутих інтегральних кривих, що містять О. т. Усередині себе, між якими розташовані спіралі (див. Мал. 10 ).

Вивчення О. т. Диференціальних рівнянь, т. Е. По суті вивчення поведінки сімейств інтегральних кривих в околиці О. т., Складає один з розділів якісної теорії диференціальних рівнянь і грає важливу роль в додатках, зокрема в питаннях стійкості руху (роботи А . М. Ляпунов а, А. Пуанкаре та ін.).

3) Особлива точка однозначної аналітичної функції - точка, в якій порушується аналітичність функції (див. Аналітичні функції). Якщо існує околиця О. т. a, Вільна від інших О. т., То точку аназивають ізольованою О. т. Якщо а- ізольована О. т. І існує кінцевий a називають усуненою О. т. Шляхом належного зміни визначення функції в точці а (або довизначення її в цій точці, якщо функція в ній взагалі не визначена), саме, вважаючи f(a)= b, Можна домогтися того, що aстане звичайною точкою виправленої функції. Наприклад, точка z= 0 є усуненою О. т. Для функції f 1 ( z) = f(z), Якщо z≠ 0, і f 1 (0), = 1, точка z= 0 є звичайною точкою [ f 1 (z) Аналітична в точці z= 0]. якщо а- ізольована О. т. І а називають полюсом або несуттєво особливою точкою функції f(z), Якщо ж Лорана ряд) функції f(z) В околиці ізольованою О. т. Не містить негативних ступенів z - а, якщо а- переборна О. т., Містить кінцеве число негативних ступенів z - а, якщо а- полюс (при цьому порядок полюса рвизначається як найвища ступінь а - істотно особлива точка. Наприклад, для функції

p = 2, 3, ...)

крапка z= 0 є полюсом порядку р, Для функції

крапка z= 0 є істотно особливою точкою.

На кордоні кола збіжності статечного ряду повинна знаходитися принаймні одна О. т. Функції, що подається всередині цього кола даними статечним поруч. Всі граничні точки області існування однозначної аналітичної функції (природного кордону) є О. т. Цієї функції. Так, всі крапки одиничного кола | z| = 1 є особливими для функції

Для багатозначної аналітичної функції поняття «Про т. » більш складно. Крім О. т., В окремих аркушах ріманової поверхні функції (тобто О. т. Однозначних аналітичних елементів) будь-яка точка розгалуження також є О. т. Функції. Ізольовані точки розгалуження римановой поверхні (тобто такі точки розгалуження, що в деякій їх околиці ні в одному аркуші немає інших О. т. Функції) класифікуються наступним чином. Якщо а - ізольована точка розгалуження кінцевого порядку і існує кінцевий а називають критичним полюсом. якщо а- ізольована точка розгалуження нескінченного порядку і а називають трансцендентною О. т. Всі інші ізольовані точки розгалуження називають критичними істотно особливими точками. Приклади: точка z= 0 є звичайною критичною точкою функції f ( z) = Ln zі критичної істотно особливою точкою функції f (z) = Sin ln z.

Будь-яка О. т., Крім усуненою, є перешкодою при аналітичному продовженні, т. Е. Аналітичне продовження вздовж кривої, що проходить через неустранимую О. т., Неможливо.

Велика Радянська Енциклопедія. - М .: Радянська енциклопедія. 1969-1978 .

Дивитися що таке "Особлива точка" в інших словниках:

Вказує сюди. Див. Також особлива точка (диференціальні рівняння). Особливість або сингулярність в математиці це точка, в якій математичний об'єкт (зазвичай функція) не визначений або має нерегулярну поведінку (наприклад, точка в якій ... ... Вікіпедія

Аналітичної функції точка, в до рій порушуються умови аналітичності. Якщо аналітіческаяфункція f (z) задана в недо рій околиці точки z0 всюди ... фізична енциклопедія

Аналітичної функції точка, в якій порушується аналітичність функції ... Великий Енциклопедичний словник

особлива точка- - [Я.Н.Лугінскій, М.С.Фезі Жилінський, Ю.С.Кабіров. Англо російський словник з електротехніки та електроенергетиці, Москва, 1999] Тематики електротехніка, основні поняття EN singular point ... Довідник технічного перекладача

1) О. т. Аналітичній функції f (z) перешкода для аналітичного продовження елемента функції f (z) комплексного змінного zвдоль будь-якого шляху на площині цього змінного. Нехай аналітична функція f (z) визначена деяким ... ... математична енциклопедія

Аналітичної функції, точка, в якій порушується аналітичність функції. * * * ОСОБЛИВА ТОЧКА ОСОБЛИВА ТОЧКА аналітичної функції, точка, в якій порушується аналітичність функції ... енциклопедичний словник

особлива точка- ypatingasis taškas statusas T sritis automatika atitikmenys: angl. singular point vok. singulärer Punkt, m rus. особлива точка, f pranc. point particulier, m; point singulier, m ... Automatikos terminų žodynas

Ряди Тейлора служать ефективним засобом для вивчення функцій, аналітичних в колі zol Для дослідження функцій, аналітичних в кільцевої області, виявляється можливим побудова розкладів по позитивним і негативним ступенями (z - zq) виду узагальнюючим Тейлоровской розкладання. Ряд (1), який розуміється як сума двох рядів називається поруч Лорана. Ясно, що областю збіжності ряду (1) є загальна частина областей збіжності кожного з рядів (2). Знайдемо її. Областю збіжності першого ряду є коло радіус якого визначається за формулою Коші-Адамара Всередині кола збіжності ряд (3) сходиться до аналітичної функції, причому в будь-якому колі меншого радіуса, він сходиться абсолютно і рівномірно. Другий ряд представляє собою статечної ряд щодо змінного Ряд (5) сходиться всередині свого кола збіжності до аналітичної функції комплексної змінної m- * oo причому в будь-якому колі меншого радіуса він сходиться абсолютно і рівномірно, ^ го означає, що областю збіжності ряду (4) є зовнішність кола - Якщо то існує загальна область збіжності рядів (3) і (4) - круговий кільце в якому ряд (1) сходиться до аналітичної функції. При цьому в будь-якому кільці, він сходиться абсолютно і рівномірно. Приклад 1. Визначити область збіжності рада Ряди Лорана Ізольовані особливі точки і їх класифікація М Область сходи мости першого ряду - зовнішність кола а область з ходи мости другого ряду - внутрішність круга Тим самим, даний ряд сходиться в коли »про Теорема 15. Будь-яку функцію f (z), однозначну і аполітичну в круговому Котьці можна уявити в цьому кільці у вигляді суми сходиться ряду коефіцієнти Сп якого визначені однозначно і обчислюються за формулами де 7р - коло радіуса м Зафіксуємо всередині кільця Я довільну точку z. Побудуємо окружності центрами в точці го, радіуси яких задовольняють нерівності і розглянемо нове кільце За інтегральною теоремою Коші для многосвязной області маємо Перетворимо окремо кожен з інтегралів в сумі (8). Для всіх точок £ по колу 7д * виконується співвідношення де суми рівномірно сходиться ряду 1 + 1 Тому дріб ^ можна уявити в ви- / "/ Помноживши обидві частини на безперервну функцію (О і проводячи почленное інтегрування уздовж окружності, отримаємо, що Перетворення другого інтеграла проведемо дещо по-іншому. Для всіх точок £ на окружності ir> виконано співвідношення Тому дріб ^ можна представити у вигляді суми рівномірно сходиться ряду Помноживши обидві частини на безперервну функцію) і інтегруючи почленно уздовж окружності 7 /, отримай м, що Зауважимо, що підінтегральна функції в формулах (10) і (12) є аналітичними функціями в круговому кільці. Тому в силу теореми Коші значення відповідних інтегралів не зміняться, якщо замінити окружності 7 / г і 7г / будь окружністю. Це дозволяє об'єднати формули (10) і (12), Замінюючи інтеграли в правій частині формули (8) їх виразами (9) і (11) відповідно, отримаємо потрібну розкладання Так як z - довільна точка кільця, то це означає, що ряд ( 14) сходиться до функції f (z) усюди в цьому кільці, причому в будь-якому кільці ряд сходиться до цієї функції абсолютно і рівномірно. Доведемо тепер, що розкладання виду (6) єдино. Припустимо, що має місце ще одне розкладання Тоді всюди всередині кільця R матимемо На окружності ряди (15) сходяться рівномірно. Помножимо обидві частини рівності (де т - фіксоване ціле число, і проинтегрируем обидва ряди почленно. В результаті отримаємо в лівій частині, а в правій - СЩ. Таким чином, (4, = У розділі ст. Так як m - довільне число, то остання рівність доводить єдиність розкладання. Ряд (6), коефіцієнти якого обчислюються поформуле (7), називається рядом Лорана функції f (z) в кільці Сукупність членів цього ряду з невід'ємними ступенями називається правильної частиною ряду Лорана, а з негативними - його головною частиною. Формули ( 7) для коефіцієнтів ряду Лорана на практиці застосовуються рідко, бо, як правило, вимагають громіздких обчислень. Зазвичай, якщо це можливо, використовуються готові Тейлоровской розкладання елементарних функцій. на підставі єдиності розкладання будь-який законний прийом призводить до одного й того ж результату. Приклад 2 . Розглянути розкладання в ряд Лорана функції різних областях, прийнявши Фуісція / (г) має дві особливі точки:. Отже, є три кільцеві област і, з центром в точці го = 0. в кожній з яких функція / (г) є аналітичної: а) коло кільце зовнішність кола (рис.27). Знайдемо лоранівські розкладання функції / (z) в кожній з цих областей. Уявімо / (z) у вигляді суми елементарних дробів а) Коло Перетворимо співвідношення (16) наступним обра- Використовуючи формулу для суми членів геометричної прогресії, отримаємо Підставами знайдені розкладання в формулу (17): Це розкладання є поруч Тейлора функції / (z). б) Кільце для функції -р залишається сходящимся в цьому кільці, так як Ряд (19) для функції j ^ j при | z | > 1 розходиться. Тому перетворимо функцію / (z) наступним чином: знову застосовуючи формулу (19), отримаємо, що Цей ряд сходиться для. Підставляючи розкладання (18) і (21) в співвідношення (20), отримаємо в) Зовнішність кола для функції -р при | z | > 2 розходиться, а ряд (21) для функ- Уявімо функцію / (z) в наступному вигляді: /<*> Використовуючи формули (18) і (19), отримаємо АБО 1 Егот приклад показує, що для однієї і тієї ж функції f (z) лоранівські розкладання, взагалі кажучи, має різний вигляд для різних кілець. Приклад 3. Знайти розкладання 8 ряд Лорана функції Ряди Лорана Ізольовані особливі точки і їх класифікація а кільцевої області А Скористаємося поданням функції f (z) в наступному вигляді: і перетворимо другий доданок Використовуючи формулу для суми членів геометрічесхой прогресії, отримаємо Підставляючи знайдені вирази в формулу (22), маємо Приклад 4. Розкласти в ряд Лорана функцію в окреслюсті тонкі zq = 0. для любою комплексного маємо Покладемо Це розкладання справедливо для будь-якої точки z Ф 0. в даному випадку кільцева область являє собою всю комплексну площину з однієї викинутої точкою z - 0. Цю область можна визначити наступним співвідношенням: Ця функція є аналітичною в області З формул (13) для коефіцієнтів ряду Лорана такими ж міркуваннями, що і в попередньому параграфі, можна отримати нерівності Kouiw. якщо функція f (z) обмежена на окружності, де М - постійна), то Ізольовані особливі точки Точка zo називається ізольованою особливою точкою функції / (z), якщо існує кільцева околиця точки (це безліч іноді називають також проколеної околицею точки 2о), в якої функція f (z) однозначна і аналітична. У самій точці zo функція або не визначена, або не є однозначною і аналітичною. Залежно від поведінки функції / (г) при наближенні до точки zo розрізняються три типи особливих точок. Ізольована особлива точка називається: 1) усуненою, якщо існує кінцевий 2) пмюсач, якщо 3) істотно особливою точкою, якщо функція f (z) не має меж при Тип ізольованою особливої ​​точки тісно пов'язаний з характером лоранівські розкладання функції виколоти центром го. Теорема 16. Ізольована особлива точка z0 функції f (z) є усуненою особливою точкою в тому і тільки в тач випадку, коли лоранівські розкладання функції f (z) в околі точки zo не містить головної частини, т. Е. Має вигляд Нехай zo - переборна особлива точка. Тоді існує кінцевий, слідів- вательно, функція f (z) обмежена впрокологой околиці точки го, Покладемо В силу нерівностей Коші Оскільки р моямо вибрати скольугодно малим, то всі коефіцієнти при негативних ступенях (z - 20) дорівнюють нулю: Назад, нехай лоранівські розкладання функції / (г) в околиці точки zq містить тільки правильну частина, т. е. має вигляд (23) і, отже, є Тейлоровской. Неважко бачити, що при z - * z0 У фуніціі / (г) існує граничне значення: Теорема 17. Ізольована особлива точка zq функції f (z) є усуненою тоді і тільки тоді, коли функція J (z) обмежена в деякій проколеної околиці точки zq, Згмечаі ні. Нехай го - переборна особлива точка функції / (г). Вважаючи ми отримаємо, чтофункція / (г) аналітична в деякому до руге з центром в точці го. Це визначає назву точки - переборна. Теорема 18. Ізольована особлива точка zq функції f (z) є полюсом в тому і тільки в тому випадку, коли головна частьлорановскогоразложенія функції f (z) в околі точки містить кінцеве (і позитивне) чіслоотлічних від нуля членів, т. Е. Має вигляд 4 Нехай z0 - полюс. Так як то існує проколота околиця точки z0, в якій функція f (z) аналітична і відмінна від нуля. Тоді в цій околиці визначена аналітична функція причому Отже, точка zq є усуненою особливою точкою (нулем) функції або де h (z) - аналітична функція, h (z0) Ф 0. Тоді аналітична і h (zo) ф 0, то функція щ аналітична в околиці точки zq, і отже, звідки отримуємо, що Припустимо тепер, що функція f (z) має в проколеної околиці точки zо розкладання виду (24). Це означає, що в цій околиці функція f (z) аналітична разом з функцією. Для функції g (z) справедливо розкладання з якого видно, що zq - переборна особлива точка функції g (z) і існує Тоді функція при 0 прагне - полюс функції Має місце ще один простий факт. Точка Zq - полюс функції f (z) в тому і тільки в тому випадку, коли функцію g (z) = ущ можна доопределить до аналітичної функції в околі точки zq, поклавши g (z0) = 0. Порядком полюса функції f (z) називається порядок нуля функції jfa. З теорем 16 і 18 випливає наступне твердження. Теорема 19. Ізольована особлива тонка є істотно особливою в тому і тільки в тому випадку, коли головна частина лоранівські розкладання в проколеної околиці цієї точки містить нескінченно багато відмінних від нуля членів. Приклад 5. Особливою точкою функції є zo = 0. Маємо Ряди Лорана Ізольовані особливі точки і їх класифікація Отже, zo = О - переборна особлива точка. Розкладання функції / (z) в ряд Лорана в околиці нульової точки містить тільки правильну частина: Прімер7. / (Г) = Особлива точка функції f (z) є zq = 0. Розглянемо поведінку цієї функції на дійсної та уявної осях: на дійсній осі при х 0, на уявної осі Отже, ні кінцевого, ні нескінченного межі f (z) при z - * 0 не існує ует. Значить, точка го = 0 - істотно особлива точка функції f (z). Знайдемо лоранівські розкладання функції f (z) в околиці нульової точки. Для будь-якого комплексного З маємо Покладемо. Тоді лоранівські розкладання містить нескінченне число членів з негативними ступенями z.

Визначення.Особлива точка функції називається ізольованою, якщо в деякій околиці цієї точки - аналітична функція (тобто аналітична в кільці).

Класифікація ізольованих особливих точок функції пов'язана з поведінкою цієї функції в околиці особливої ​​точки.

Визначення.точка називається усуненою особливою точкою функції, якщо існує кінцева межа цієї функції при.

Приклад 5.Показати, що функція має в точці переборні особливість.

Рішення.Згадуючи перший чудовий межа, обчислимо

Значить, в точці задана функція має переборні особливість.

Завдання 4.Показати, що точка переборна для.

Визначення.точка називається полюсом функції, якщо ця функція необмежено зростає при, тобто.

Звернемо увагу на зв'язок між поняттями нуля і полюса аналітичної функції. Уявімо функцію у вигляді.

Якщо точка є простим нулем функції, то функція має в простий полюс

Якщо точка - нуль порядку для функції, то для функції це полюс порядку.

Приклад 6.Показати, що функція має в точці полюс третього порядку.

Рішення.Вважаючи, отримаємо. При прагненні до нуля з будь-якого закону маємо. Тоді, а з ним і сама функція необмежено зростає. Отже,, тобто особлива точка є полюсом. Для функції ця точка, очевидно, є триразовим нулем. Значить, для даної функції точка є полюсом третього порядку.

Завдання 5.Показати, що в точці має простий полюс.

Визначення.точка називається істотно особливої точкою функції, якщо в цій точці не існує ні кінцевого, ні нескінченного границі функції (поведінка функції не визначено).

Нехай є істотно особливою точкою функції. Тоді для будь-якого наперед заданого комплексного числа знайдеться така послідовність точок, що сходиться до, уздовж якої значення прагнуть до: ( теорема Сохоцкого).

Приклад 7.Показати, що функція в точці має істотну особливість.

Рішення.Розглянемо поведінку заданої функції в околі точки. При уздовж позитивної частини дійсної осі (тобто) маємо і; якщо ж уздовж негативній частині дійсної осі (тобто), то і. Значить, не існує межі прі. За визначенням, в точці функція має істотну особливість.

Розглянемо поведінку функції в нулі з точки зору теореми Сохоцкого. Нехай - будь-яке комплексне число, відмінне від нуля і нескінченності.

З рівності знаходимо. Вважаючи, отримаємо послідовність точок,. Очевидно,. У кожній точці цієї послідовності функція дорівнює, тому і

Завдання 6.Показати, що функція має в точці істотну особливість.

Нескінченно віддалена точка завжди вважається особливою для функції. Точка називається ізольованою особливою точкою функції, якщо ця функція поза деякого кола з центром на початку координат не має інших особливих точок.

Класифікацію ізольованих особливих точок можна поширити і на випадок.

Приклад 8.Показати, що функція має на нескінченності дворазовий полюс.

Рішення.Розглянемо функцію, де - аналітична функція в околі точки, причому. Значить, функція має на нескінченності дворазовий нуль, але тоді для функції точка є дворазовим полюсом.

Приклад 9.Показати, що функція має на нескінченності істотну особливість.

Рішення.Аналогічне завдання розглянута в пр.7. Розглянемо поведінку функції в околиці нескінченно віддаленої точки. При уздовж позитивної частини дійсної осі, а при уздовж негативній частині дійсної осі. Значить, не існує межі функції в точці і в силу визначення ця точка - істотно особлива.

Про характер особливості функції в точці можна судити по головної частини лоранівські розкладання в околиці цієї точки.

Теорема 1.Для того щоб точка була усуненою особливою точкою функції, необхідно і достатньо, щоб відповідне лоранівські розкладання не містило головної частини.

Завдання 6.Користуючись Тейлоровской розкладанням функції в околі точки, показати, що має в нулі переборні особливість.

Теорема 2.Для того щоб точка була полюсом функції, необхідно і достатньо, щоб Головна частина відповідного лоранівські розкладання містила кінцеве число членів :

Номер старшого негативного члена визначає порядок полюса.

У цьому випадку функцію можна представити у вигляді

де - аналітична в точці функція,, - порядок полюса.

Приклад 10.Показати, що функція має в точках і прості полюси.

Рішення.Розглянемо точку. Скористаємося лоранівські розкладанням цієї функції в околиці цієї точки, отриманим в прикладі 2:

Так як в головній частині цього розкладання старша (і єдина) негативна ступінь дорівнює одиниці, то точка - простий полюс даної функції.

Можна було отримати цей результат іншим шляхом. Уявімо у вигляді і покладемо - це функція, аналітична в точці і. Значить, і в силу (8) в точці дана функція має простий полюс.

Ще один спосіб: розглянемо функцію, яка в точці має простий нуль. Значить, в цій точці має простий полюс.

Аналогічно, якщо записати функцію в вигляді, де - функція, аналітична в точці і, то відразу ясно, що точка - простий полюс функції.

Завдання 7.Показати, що функція має полюс 2 -го порядку в точці і полюс 4 -го порядку в точці.

Теорема 3.Для того щоб точка була істотно особливої точкою функції, необхідно і достатньо, щоб Головна частина лоранівські розкладання в околиці точки містила нескінченне число членів .

Приклад 11.Визначити характер особливості в точці функції

Рішення.У відомому розкладанні косинуса покладемо замість:

Значить, лоранівські розкладання в околиці точки має вигляд

Тут правильна частина - один доданок. А головна частина містить нескінченне число доданків, тому точка - істотно особлива.

Завдання 8.Показати, що в точці функція має істотну особливість.

Розглянемо деяку функцію і запишемо її лоранівські розкладання в точці:

Зробимо заміну, при цьому точка переходить в точку. Тепер в околиці нескінченно віддаленої точки маємо

Залишилося ввести нове позначення. отримуємо

де - головна частина, а - правильна частина лоранівські розкладання функції в околиці нескінченно віддаленої точки. Таким чином, в лоранівські розкладанні функції в околиці точки головна частина - це ряд по позитивним ступенями, а правильна частина - ряд по негативним ступенями. З огляду на це заме

чания наведені критерії для визначення характеру особливості залишаються в силі і для нескінченно віддаленої точки.

Приклад 12.З'ясувати характер особливості функції в точці. , То в точці може виявитися неізольованою.

Приклад 15.Функція в нескінченно віддаленій точці має істотну особливість. Показати, що точка для функції не є ізольованою особливою точкою.

Рішення.Функція має безліч полюсів в нулях знаменника, тобто в точках,. Так як, то точка, в будь-який околиці якої є полюси, є граничною для полюсів.

Моделі, що описуються системами двох автономних диференціальних рівнянь.

Фазова площина. Фазовий портрет. Метод ізоклін. Головні ізокліни. Стійкість стаціонарного стану. Лінійні системи. Типи особливих точок: вузол, сідло, фокус, центр. Приклад: хімічні реакції першого порядку.

Найбільш цікаві результати по якісному моделюванню властивостей біологічних систем отримані на моделях з двох диференціальних рівнянь, які допускають якісне дослідження за допомогою методу фазової площини. Розглянемо систему двох автономних звичайних диференціальних рівнянь загального вигляду

(4.1)

P (x, y), Q (x, y)- безперервні функції, визначені в деякій області Gевклідової площині ( x, y- декартові координати) і мають в цій області безперервні похідні порядку не нижче першого.

область Gможе бути як необмеженої, так і обмеженою. якщо змінні x, yмають конкретний біологічний сенс (концентрації речовин, чисельності видів) найчастіше область Gє позитивний квадрант правій півплощині:

0 £ x< ¥ ,0 £ y< ¥ .

Концентрації речовин або чисельності видів також можуть бути обмежені зверху об'ємом посудини або площею ареалу проживання. Тоді область значень змінних має вигляд:

0 £ x< x 0 , 0 £ y< y 0 .

змінні x, yв часі змінюються відповідно до системи рівнянь (4.1), так що кожному стану системи відповідає пара значень змінних ( x, y).

Назад, кожній парі змінних ( x, y) Відповідає певний стан системи.

Розглянемо площину з осями координат, на яких відкладені значення змінних x, y. кожна точка Мцій площині відповідає певному стану системи. Така площину зветься фазової площини і зображує сукупність всіх станів системи. Точка М (x, y) називається зображає або представляє точкою.

Нехай в початковий момент часу t = t 0 координати зображає точки М 0 (x(t 0), y(t 0)). У кожен наступний момент часу tзображає точка буде зміщуватися відповідно до змін значень змінних x(t), y(t). сукупність точок М(x(t), Y (t)) На фазовій площині, положення яких відповідає станам системи в процесі зміни в часі змінних x (t), y (t)відповідно до рівнянь (4.1), називається фазової траєкторією.

Сукупність фазових траєкторій при різних початкових значеннях змінних дає легко доступний для огляду "портрет" системи. побудова фазового портретадозволяє зробити висновки про характер змін змінних x, yбез знання аналітичних рішень вихідної системи рівнянь(4.1).

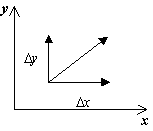
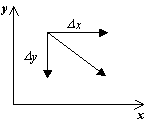
Для зображення фазового портрета необхідно побудувати векторне поле напрямків траєкторій системи в кожній точці фазової площини. ставлячи прирістD t> 0,отримаємо відповідні збільшення D xі D yз виразів:

D x = P (x, y)D t,

D y = Q (x, y)D t.

напрямок вектора dy / dxв точці ( x, y) Залежить від знака функцій P (x, y), Q (x, y)і може бути задано таблицею:

P (x, y)> 0, Q (x, y)> 0
P (x, y)<0,Q(x,y)<0
P (x, y)> 0, Q (x, y)<0
P (x, y)<0,Q(x,y)>0

.(4.2)

Рішення цього рівняння y = y(x, c), або в неявному вигляді F(x, y)= C,де з- постійна інтегрування, дає сімейство інтегральних кривих рівняння (4.2) - фазових траєкторійсистеми (4.1) на площині x, y.

метод ізоклін

Для побудови фазового портрета користуються методом ізоклін -на фазової площині наносять лінії, які перетинають інтегральні криві під одним певним кутом. Рівняння ізоклін легко отримати з (4.2). покладемо

де А– певна постійна величина. значення Аявляє собою тангенс кута нахилу дотичної до фазової траєкторії і може приймати значення від -¥ до + ¥ . підставляючи замість dy / dxв (4.2) величину Аотримаємо рівняння ізоклін:

.(4.3)

Рівняння (4.3) визначає в кожній точці площини єдину дотичну до відповідної інтегральної кривої за винятком точки, де P (x, y)= 0, Q (x, y) = 0 , В якій напрям дотичній стає невизначеним, тому що при цьому стає невизначеним значення похідної:

.

Ця точка є точкою перетину всіх ізоклін - особливою точкою.У ній одночасно звертаються в нуль похідні за часом змінних xі y.

Таким чином, в особливій точці швидкості зміни змінних дорівнюють нулю. Отже, особлива точка диференціальних рівнянь фазових траєкторій (4.2) відповідає стаціонарного стану системи(4.1), а її координати - суть стаціонарні значення змінних x, y.

Особливий інтерес представляють головні ізокліни:

dy / dx = 0, P(x, y)=0 – ізокліни горизонтальних дотичних і

dy / dx =¥ , Q(x, y)=0 – ізокліни вертикальних дотичних.

Побудувавши головні ізокліни і знайшовши точку їх перетину (X, y), Координати якої задовольняють умовам:

ми знайдемо тим самим точку перетину всіх ізоклін фазової площини, в якій напрям дотичних до фазових траєкторіях невизначено. це - особлива точка, Яка відповідає стаціонарного стану системи(Рис. 4.2).

Система (4.1) має стількома стаціонарними станами, скільки точок перетину головних ізоклін є на фазової площині.

Кожна фазова траєкторія відповідає сукупності рухів динамічної системи, що проходять через одні й ті ж стану і відрізняються один від одного тільки початком відліку часу.

Якщо умови теореми Коші виконані, то через кожну точку простору x, y, tпроходить єдина інтегральна крива. Те ж справедливо, завдяки автономності, для фазових траєкторій: через кожну точку фазової площини проходить єдина фазова траєкторія.

Стійкість стаціонарного стану

Нехай система перебуває в стані рівноваги.

Тоді зображає точка знаходиться в одній з особливих точок системи, в яких за визначенням:

.

Стійка чи ні особлива точка, визначається тим, піде чи ні зображає точка при малому відхиленні від стаціонарного стану. Стосовно до системи з двох рівнянь визначення стійкості на мовіe, dвиглядає наступним чином.

Стан рівноваги стійко, якщо для будь-якої заданої області відхилень від стану рівноваги (e )можна вказати область d (e ), Навколишнє стан рівноваги і володіє тим властивістю, що жодна траєкторія, яка починається всередині області d , Ніколи не досягне межі e . (Рис. 4.4)

Для великого класу систем - грубих систем – характер поведінки яких не змінюється при малій зміні виду рівнянь, інформацію про тип поведінки в околиці стаціонарного стану можна отримати, досліджуючи НЕ вихідну, а спрощену лінеаризованусистему.

Лінійні системи.

Розглянемо систему двох лінійних рівнянь:

.(4.4)

тут a, b, c, d- константи, x, y- декартові координати на фазової площині.

Загальне рішення будемо шукати у вигляді:

.(4.5)

Подставіметі вираження в (4.4) і скоротимо на e l t:

(4.6)

Алгебраїчна система рівнянь (4.6) з невідомими A, Bмає нульове рішення лише в тому випадку, якщо її визначник, складений з коефіцієнтів при невідомих, дорівнює нулю:

.

Розкриваючи цей визначник, отримаємо характеристичне рівняння системи:

.(4.7)

Рішення цього рівняння дає значення показникаl 1,2 , При яких можливі ненульові для Aі Bрішення рівняння (4.6). Ці значення суть

.(4.8)

Якщо подкоренное вираз негативно, тоl 1,2 комплексно зв'язані числа. Припустимо, що обидва кореня рівняння (4.7) мають відмінні від нуля дійсні частини і що немає кратних коренів. Тоді загальне рішення системи (4.4) можна представити у вигляді лінійної комбінації експонент з показникамиl 1 , l 2 :

(4.9)

Для аналізу характеру можливих траєкторій системи на фазовій площині використовуємо лінійне однорідне перетворення координат,яке дозволить привести систему до канонічного виду:

,(4.10)

допускає більш зручне представлення на фазової площині в порівнянні з вихідною системою (4.4). Введемо нові координатиξ , η за формулами:

(4.1)

З курсу лінійної алгебри відомо, що в разі нерівності нулю дійсних частинl 1 , l 2 вихідну систему (4.4) за допомогою перетворень (4.11) завжди можна перетворити до канонічного вигляду (4.10) і вивчати її поведінку на фазової площиніξ , η . Розглянемо різні випадки, які можуть тут бути.

коріння λ 1 , λ 2 - дійсні й одного знака

В цьому випадку коефіцієнти перетворення дійсні, ми переходимо від дійсної площиниx, yдо дійсної площини ξ, η. Розділивши друге з рівнянь (4.10) на перше, отримаємо:

.(4.12)

Інтегруючи це рівняння, знаходимо:

Де. (4.13)

Домовимося розуміти під λ 2 корінь характеристичного рівняння з великим модулем, що чи не порушує спільності нашого міркування. Тоді, оскільки в даному випадку коріння λ 1 , λ 2 - дійсні й одного знака,a>1 , І ми маємо справу з інтегральними кривими параболічного типу.

Всі інтегральні криві (крім осі η , Якій відповідає ) Стосуються в початку координат осі ξ, яка також є інтегральною кривою рівняння (4.11). Початок координат є особливою точкою.

З'ясуємо тепер напрямок рухів зображає точки вздовж фазових траєкторій. якщо λ 1, λ 2 - негативні, то, як видно з рівнянь (4.10), | ξ |, | η | зменшуються з плином часу. Зображає точка наближається до початку координат, ніколи, однак, не досягаючи його. В іншому випадку це суперечило б теоремі Коші, яка стверджує, що через кожну точку фазової площини проходить лише одна фазова траєкторія.

Така особлива точка, через яку проходять інтегральні криві, подібно до того, як сімейство парабол проходить через початок координат, носить назву вузла (рис. 4.5)

Стан рівноваги типу вузол при λ 1, λ 2 < 0 стійко по Ляпунову, так як зображає точка по всьому інтегральним кривим рухається у напрямку до початку координат. це стійкий вузол. Якщо ж λ 1, λ 2 > 0, то | Ξ |, | η | зростають з плином часу і зображає точка віддаляється від початку координат. В цьому випадку особлива точка– нестійкий вузол .

На фазовій площині x, y загальний якісний характер поведінки інтегральних кривих збережеться, але дотичні до інтегральним кривим не збігатимуться з осями координат. Кут нахилу цих дотичних буде визначатися співвідношенням коефіцієнтів α , β , γ , δ в рівняннях (4.11).

коріння λ 1 , λ 2 - дійсні і різних знаків.

перетворення відкоординат x, y до координат ξ, η знову дійсне. Рівняння для канонічних змінних знову мають вигляд (4.10), але тепер знаки λ 1, λ 2 різні. Рівняння фазових траєкторій має вигляд:

Де, (4.14)

Інтегруючи (4.14), знаходимо

(4.15)

це рівняння визначає сімейство кривих гіперболічного типу, де обидві осі координат- асимптоти (при a=1 ми мали б сімейство равнобочной гіпербол). Осі координат і в цьому випадку є інтегральними кривими– це будуть єдині інтегральні криві, що проходять через початок координат. кожназ них складається з трьох фазових траєкторій: з двох рухів до стану рівноваги (або від стану рівноваги) і зі стану рівноваги. Всі інші інтегральні криві– суть гіперболи, що не проходять через початок координат (рис. 4.6) Така особлива точка називається «сідло ». Лінії рівня поблизу гірської сідловини поводяться подібно фазовим траєкторіях в околиці сідла.

Розглянемо характер руху зображає точки по фазовим траєкторіях поблизу стану рівноваги. Нехай, наприклад,λ 1> 0, λ 2<0 . Тоді зображає точка, вміщена на осі ξ , Буде віддалятися від початку координат, а поміщена на осі η – буде необмежено наближатися до початку координат, не досягаючи його за кінцевий час. Де б не знаходилася зображає точка в початковий момент (за винятком особливої ​​точки і точок на асимптоти η =0), вона в кінцевому рахунку буде віддалятися від стану рівноваги, навіть якщо на початку вона рухається по одній з інтегральних кривих у напрямку до особливої ​​точки.

Очевидно, що особлива точка типу сідла завжди нестійка . Тільки при спеціально обраних початкових умовах на асимптотиη =0 система буде наближатися до стану рівноваги. Однак це не суперечить твердженням про нестійкість системи. якщо вважати, що все початкові стану системи на фазовій площині різновірогідні, то ймовірність такого початкового стану, яке відповідає руху у напрямкудо особливій точці, дорівнює нулю. Тому будь-яке реальне рух буде видаляти систему від стану рівноваги.Переходячи назад до координатx, y,ми отримаємо ту ж якісну картину характеру руху траєкторій навколо початку координат.

Прикордонним між розглянутими випадками вузла і сідла є випадок,коли один з характеристичних показників, наприклад λ 1 , звертається в нуль, що має місце, коли визначник системи- вираз ad-bc = 0(Див. Формулу 4.8 ). В цьому випадку коефіцієнти правих частин рівнянь (4.4) пропорційні один одному:

і система має своїми станами рівноваги всі точки прямої:

Решта інтегральні криві представляють собою сімейство паралельних прямих з кутовим коефіцієнтом , За якими зображують точки або наближаються до стану рівноваги, або віддаляються від нього в залежності від знака другого кореня характеристичного рівняння λ 2 = a + d.(Рис.4. 7 ) У цьому випадку координати стану рівноваги залежать від початкового значення змінних.

коріння λ 1 , λ 2 – комплексніпов'язані

В цьому випадку при дійснихxі yми будемо мати комплексні пов'язані ξ , η (4.10) . Однак, вводячи ще одна проміжна перетворення, можна і в цьому випадку звести розгляд до дійсного лінійному однорідному перетворенню. покладемо:

(4.16)

де a, b,і u, v – дійсні величини. Можна показати, що перетворення відx, yдо u, v є при наших припущеннях дійсним, лінійним, однорідним з детермінантою, відмінним від нуля. В силу рівнянь(4.10, 4.16) маємо:

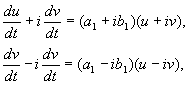
звідки

(4.17)

Розділивши друге з рівнянь на перше, Отримаємо:

яке легше інтегрується, якщо перейти до полярної системі координат (r, φ ) . після підстановкиотримаємо, звідки:

.(4.18)

Таким чином, на фазовій площиніu, vми маємо справу з сімейством логарифмічних спіралей, кожна з яких маєасимптотическую точку на початку координат.Особлива точка, яка є асимптотической точкою всіх інтегральних кривих, що мають вигляд спіралей, вкладених один вдруга, називається фокусом ( рис.4.8 ) .

Розглянемо характер руху зображає точки по фазовим траєкторіях. Помноживши перше з рівнянь (4.17) наu, А друге на vі складаючи, отримуємо:

де

нехай a 1 < 0 (a 1 = Reλ ) . Зображає точка тоді безперервно наближається до початку координат, не досягаючи його в кінцевий час. Це означає, що фазові траєкторії являють собою скручуються спіралі і відповідають загасаючим коливаньзмінних. це - стійкий фокус .

У разі стійкого фокуса, як і в разі стійкого вузла, виконано не тільки умова Ляпунова, але і більш жорстку вимогу. Саме, при будь-яких початкових відхиленнях система з часом повернеться як завгодно близько до положення рівноваги. Така стійкість, при якій початкові відхилення не тільки не наростають, але загасають, прагнучи до нуля, називають абсолютною стійкістю .

Якщо у формулі (4.18) a 1 >0 , То зображає точка віддаляється від початку координат, і ми маємо справу з нестійким фокусом . При переході від площиниu, vдо фазової площиниx, yспіралі також залишаться спіралями, проте будуть деформовані.

Розглянемо тепер випадок, колиa 1 =0 . Фазовими траєкторіями на площиніu, vбудуть окружності яким на площиніx, yвідповідають еліпси:

Таким чином, приa 1=0 через особливу точкуx = 0, Y = 0 не проходить жодна інтегральна крива. Така ізольована особлива точка, поблизу якої інтегральні криві представляють собою замкнуті криві, зокрема, еліпси, вкладені одна в одну і охоплюють особливу точку, називається центром.

Таким чином, можливі шість типів стану рівноваги в залежності від характеру коренів характеристичного рівняння (4.7). Вид фазових траєкторій на площині x, yдля цих шести випадків зображений на рис. 4.9.

Мал. 4.9.Типи фазових портретів в околиці стаціонарного стану для системи лінійних рівнянь (4.4).

П'ять типів стану рівноваги грубі, їх характер не змінюється при досить малих змінах правих частин рівнянь (4.4). При цьому малими повинні бути зміни не тільки правих частин, а й їх похідних першого порядку. Шосте стан рівноваги - центр - негрубі. При малих змінах параметрів правій частині рівнянь він переходить в стійкий або нестійкий фокус.

біфуркаційних діаграма

Введемо позначення:

. (4.11)

Тоді характеристичне рівняння запишеться у вигляді:

. (4.12)

Розглянемо площину з прямокутними декартовими координатами s , D і відзначимо на ній області, які відповідають тому чи іншому типу стану рівноваги, який визначається характером коренів характеристичного рівняння

.(4.13)

Умовою стійкості стану рівноваги буде наявність негативної дійсної частини уl 1 і l 2 . Необхідна і достатня умова цього - виконання нерівностейs > 0, D > 0 . На діаграмі (4.15) цій умові відповідають точки, розташовані в першій чверті площини параметрів. Особлива точка буде фокусом, якщоl 1 і l 2 комплексні. Цій умові відповідають ті точки площині, для яких , тобто точки між двома гілками параболиs 2 = 4 D. точки піввісь s = 0, D> 0, відповідають станам рівноваги типу центр. аналогічно,l 1 і l 2 - дійсні, але різних знаків, тобто особлива точка буде сідлом, якщо D<0, і т.д. У підсумку ми отримаємо діаграму розбиття площині параметрів s, D, На області, які відповідають різним типам стану рівноваги.

Мал. 4.10.біфуркаційних діаграма

для системи лінійних рівнянь 4.4

Якщо коефіцієнти лінійної системи a, b, c, dзалежать від деякого параметра, то при зміні цього параметра будуть змінюватися і величиниs , D . При переході через кордони характер фазового портрета якісно змінюється. Тому такі кордону називаються біфуркаційних - по різні боки від кордону система має два топологічно різних фазових портрета і, відповідно два різних типи поведінки.

На діаграмі видно, як можуть проходити такі зміни. Якщо виключити особливі випадки - початок координат, - то легко бачити, що сідло може переходити в вузол, стійкий або нестійкий при перетині осі ординат. Стійкий вузол може перейти або в сідло, або в стійкий фокус, і т.д. Відзначимо, що переходи стійкий вузол - стійкий фокус і нестійкий вузол - нестійкий фокус не є біфуркаційних, так як топологія фазового простору при цьому не змінюється. Більш детально ми поговоримо про топології фазового простору і біфуркаційних переходах в лекції 6.

При біфуркаційних переходах змінюється характер стійкості особливої ​​точки. Наприклад, стійкий фокус через центр може переходити в нестійкий фокус. Ця біфуркація називається біфуркацією Андронова-Хопфапо іменах досліджували її вчених. При цій біфуркації в нелінійних системах відбувається народження граничного циклу, і система стає автоколебательной (див. Лекцію 8).

Приклад. Система лінійних хімічних реакцій

речовина Хпритікає ззовні з постійною швидкістю, перетворюється в речовину Y і зі швидкістю, пропорційною концентрації речовини Y, Виводиться зі сфери реакції. Всі реакції мають перший порядок, за винятком припливу речовини ззовні, має нульовий порядок. Схема реакцій має вигляд:

(4.14)

і описується системою рівнянь:

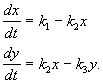(4.15)

Стаціонарні концентрації отримаємо, прирівнявши праві частини нулю:

.(4.16)

Розглянемо фазовий портрет системи. Розділимо друге рівняння системи (4.16) на перше. отримаємо:

.(4.17)

Рівняння (4.17) визначає поведінку змінних на фазової площині. Побудуємо фазовий портрет цієї системи. Спочатку намалюємо головні ізокліни на фазової площині. Рівняння ізокліни вертикальних дотичних:

Рівняння ізокліни горизонтальних дотичних:

Особлива точка (стаціонарний стан) лежить на перетині головних ізоклін.

Тепер визначимо, під яким кутом перетинаються координатні осі інтегральними кривими.

якщо x = 0, то.

Таким чином, тангенс кута нахилу дотичної до інтегральним кривим y = y (x),перетинають вісь ординат x = 0, Негативний у верхній півплощині (згадаємо, що змінні x, yмають значення концентрацій, і тому нас цікавить тільки правий верхній квадрант фазової площині). При цьому величина тангенса кута нахилу дотичної збільшується з віддаленням від початку координат.

Розглянемо вісь y = 0. У місці перетину цієї осі інтегральними кривими вони описуються рівнянням

при тангенс кута нахилу інтегральних кривих, які перетинають вісь абсцис, позитивний і збільшується від нуля до нескінченності зі збільшенням x.

При.

Потім при подальшому збільшенні тангенс кута нахилу зменшується за абсолютною величиною, залишаючись негативним і прагне до -1 при x ® ¥ . Знаючи напрямок дотичних до інтегральним кривим на головних ізокліни і на осях координат, легко побудувати всю картину фазових траєкторій.

Характер стійкості особливої ​​точки встановимо, користуючись методом Ляпунова. Характеристичний визначник системи має вигляд:

.

Розкриваючи визначник, отримаємо характеристичне рівняння системи: , Тобто корені характеристичного рівняння обидва негативні. Отже, стаціонарний стан системи являє собою стійкий вузол. При цьому концентрація речовини Xпрагне до стаціонарного стану завжди монотонно, концентрація речовини Y може проходити через min або max. Коливальні режими в такій системі неможливі.

Основні поняття і визначення:

Нулем аналітичної функції f (z) називається точка "a", для якої f (a) = 0.

Нулем порядку "n" функції f (z) називається точка «а», якщо але fn (a) ¹0.

Особлива точка «a» називається ізольованою особливою точкою функції f (z), якщо існує околиця цієї точки, в якій немає особливих точок, крім «a».

Ізольовані особливі точки бувають трьох типів:.

1 переборні особливі точки;

3 істотно особливі точки.

Тип особливої ​​точки може бути визначений виходячи з поведінки даної функції в знайденої особливій точці, а також з виду ряду Лорана, отриманого для функції в околиці знайденої особливої ​​точки.

Визначення типу особливої ​​точки з поведінки функції в ній.

1.Устранімие особливі точки.

Ізольована особлива точка a функції f (z) називається усуненою, якщо існує кінцева межа.

2.Полюси.

Ізольована особлива точка a функції f (z) називається полюсом, якщо .

3. Істотною особливі точки.

Ізольована особлива точка a функції f (z) називається істотно особливою точкою, якщо не існує ні кінцевий, ні нескінченний.

Між нулями і полюсами функції має місце наступна зв'язок.

Для того, щоб точка a була полюсом порядку n функції f (Z), необхідно і достатньо, щоб ця точка була нулем порядку n для функції.

Якщо n = 1 полюс називається простим.

визначення:Ізольована особлива точка однозначного характеру називається:

а) усуненою, якщо головна частина розкладання відсутня;

б) полюсом, якщо головна частина містить кінцеве число членів;

в) істотно особливою точкою, якщо головна частина містить нескінченне число членів.

а) Таким чином, в околиці усуненою особливої ​​точки розкладання має вигляд:

воно висловлює функцію у всіх точках кола | z-a |

У центрі z = a рівність невірно, тому що функція при z = a має розрив, а права частина безперервна. Якщо в центрі значення функції змінити, прийнявши його рівним значенню правій частині, то розрив буде устранен- звідси і назва - усувний.

б) В околиці полюса порядку m розкладання в ряд Лорана має вигляд:

в) В околиці простого полюса

Відрахування та формули для їх обчислення.

Вирахуванням аналітичної функції f (z) в ізольованій особливій точці z 0 називається комплексне число, що дорівнює значенню інтеграла , Взятого в позитивному напрямку по колу L з центром в точці z 0, що лежить в області аналітичності функції f (z) (тобто в кільці 0<|z-z0|

Позначається відрахування функції f (z) в ізольованій особливій точці z 0 символом Res f (z 0) або Res (f (z); z 0). Таким чином,

Res f (z 0) = . (22.15.1)

Якщо у формулі (22.15.1) покласти n = -1, то отримаємо:

C 1 =

або Res f (z 0) = C -1,

тобто відрахування функції f (z) щодо особливої ​​точки z 0 рівний коефіцієнту при першому члені з негативним показником в розкладанні функції f (z) в ряд Лорана.

Обчислення відрахувань.

Правильні чи переборні особливі точки. Очевидно, якщо z = z 0 є правильна або переборна особлива точка функції f (z), то Res f (z 0) = 0 (в розкладанні Лорана в цих випадках відсутня головна частина, тому c-1 = 0).

Полюс. Нехай точка z 0 є простим полюсом функції f (z). Тоді ряд Лорана для функції f (z) в околі точки z 0 має вигляд:

Звідси

Тому, переходячи в цій рівності до межі при z --z 0, отримуємо

Res f (z0) =

Істотно особлива точка. Якщо точка z 0 - істотно особлива точка функції f (z), то для обчислення вирахування функції в цій точці зазвичай безпосередньо визначають коефіцієнт c-1 в розкладанні функції в ряд Лорана.

Класифікація подій. Сума, твір подій, їх властивості, графічне представлення.

Події діляться на:

1. Випадкові

2. Достовірні

3. Неможливі

Достовірне - це така подія, яка настає обов'язково в даних умовах (за вночі слід ранок).

Випадкове - це така подія, яка може відбутися, а може і не відбутися (здача іспиту).

Неможливе - це така подія, яка в даних умовах не наступить (дістати зелений олівець з коробки тільки з червоними).